مبتنی بر مدلسازی – نظریه بازی

چیستی نظریۀ بازی

نظریه بازی حوزه‌ای نسبتاً جدید از ریاضیات است که به مدل‌سازی و تحلیل بازی‌ها می‌پردازد. منظور از بازی هر موقعیتی است که در آن تصمیم‌گیرندگانی که کنشگر آن موقعیت هستند با یکدیگر تعامل (همکاری یا رقابت) می‌کنند. برای مثال شرکت‌هایی که در بازارِ یک محصول خاص با یکدیگر رقابت می‌کنند، جانورانی که برای تسلط بر یک محدوده جغرافیایی با منابع غذایی محدود مجبورند منازعه کنند، شرکت‌کنندگان یک حراج که می‌خواهند حراج را ببرند، نامزدهای سیاسی که هرکدام می‌خواهند پیروز میدان شوند، اعضای هیئت‌منصفه که بارأی خود در دادگاه در نتیجه حکم تأثیر می‌گذارند، همگی مثال‌هایی از بازیگران تصمیم‌گیرنده در یک بازی هستند که نتیجه تصمیمشان وابسته به تصمیم دیگران است.

هر تصمیمی که یک فرد در زندگی خود می‌گیرد لزوماً به این معنا او را در موقعیت یک بازی قرار نمی‌دهد. برای مثال فرض کنید فردی بخواهد یک لپ‌تاپ بخرد و مشخصاتی که برای او اهمیت دارند به ترتیب اولویت کاملاً مشخص‌اند. از طرف دیگر دو مدل لپ‌تاپ وجود دارند که این مشخصات در هر دو مدل نیز کاملاً قابل رصد و ارزیابی هستند. هنگامی‌که این فرد می‌خواهد تصمیم به خرید بگیرد، با یک مسأله تصمیم‌گیری محض روبه‌روست. در این مورد تصمیم‌گیرنده نیازی به لحاظ کردن تصمیم فرد ذی‌شعور دیگری ندارد و می‌تواند با محاسبات ریاضی دقیقاً مشخص کند که کدام انتخاب ارزش بیشتری برای او دارد. پس این‌یک بازی نیست؛ اما در مثال‌های قبلی چنین نیست. برای مثال فردی که در یک حراج شرکت می‌کند مستقل از دیگران پیشنهاد نمی‌دهد؛ بلکه این را نیز در ذهن خود محاسبه می‌کند که دیگر شرکت‌کنندگان احتمالاً چه پیشنهادی خواهند داد و با توجه به این موضوع تصمیم می‌گیرد؛ بنابراین کنشگر در یک بازی باید بداند که «اگر بازیگر اول و دوم و … و -nام به ترتیب x₁ و x₂ و … و xₙ را انتخاب کنند، بهترین انتخاب من چه خواهد بود». وقتی مجموعه همه این حالات در نظر گرفته شوند فرد یک استراتژی دارد.

تاریخچۀ نظریۀ بازی

گرچه مسائل ریاضی مرتبط با تحلیل بازی‌ها تاریخچه‌ای سیصدساله دارند، اما تا قبل از قرن بیستم، حوزه‌ای مستقل بانام نظریه بازی وجود نداشت. این حوزه با انتشار کتابی بانام نظریه بازی‌ها و رفتار اقتصادی[1]نوشته جان فون‌نویمان[2] و اسکار مورگن‌استرن[3] شروع به شکل‌گیری کرد. از دهه پنجاه میلادی، دستاوردهای نظریه بازی در حوزه‌های دیگری مانند علوم سیاسی و اقتصاد و زیست‌شناسی به کار گرفته شد و نتایج پرباری داشت؛ برای مثال در سال 1994 به جان نش[4]، جان هارشنی[5] و راینهارت زِلتِن[6] مشترکاً جایزه نوبل اقتصاد تعلق گرفت. نَش با تمایز قائل شدن بین بازی‌های همکارانه[7] و غیرهمکارانه، ثابت کرد در همه بازی‌های غیرهمکارانه نقطه تعادلی وجود دارد که بعدازآن به تعادل نش[8] معروف شد. هارشنی تحلیلی از بازی‌های با اطلاعات ناکامل[9] ارائه داد. زلتن از مفهوم تعادل نش دربازی‌هایی استفاده کرد که در آن‌ها تعاملات استراتژیک پویا[10] وجود دارد.

انواع بازی‌ها

طبق تقسیم‌بندی‌های متفاوت، بازی‌ها انواع مختلفی دارند.‌ در اینجا سه نوع تقسیم‌بندی بازی‌ها معرفی می‌شوند. در تقسیم‌بندی اول، به سود و زیانی که درنهایت به بازیگران می‌رسد، توجه می‌شود. فرض کنید سود و زیان به ترتیب اعدادی با علامت‌های مثبت و منفی در نظر گرفته شوند. اگر در یک بازی جمع همه این اعداد صفر شود، به آن بازی جمع-صفر[11] و در غیر این صورت به آن جمع-ناصفر گویند. برای مثال در یک بازی جمع-صفر دو نفرِ، هر مقداری که یکی از بازیگران ببازد، حتماً بازیگر دیگر آن را برده است.

تقسیم‌بندی دوم، میزان اطلاعات بازیگران از قواعد بازی را در نظر می‌گیرد. اگر همه بازیگران از حرکات ممکن یکدیگر و سود و زیانی که از آن‌ها برای هر یک حاصل می‌شود آگاه باشند، بازی با اطلاعات کامل[12] است. در حالتی که این اطلاعات ناکامل باشد – مثلاً در حراجی که فرد نمی‌داند چه تعداد پیشنهاددهنده دیگر برای قیمت حضور دارند – بازیگران نمی‌دانند دقیقاً در چه بازی شرکت می‌کنند و برای آن‌که بتوانند بهترین تصمیم را بگیرند، مجبورند اطلاعات خود را به نحوی تکمیل کنند.

تقسیم‌بندی سوم مربوط به این است که حرکات بازیگران مرحله‌به‌مرحله انجام می‌شود یا هم‌زمان. در حالت اول که به آن بازی ترتیبی[13] گفته می‌شود، هر بازیگر در نوبت خود حرکتی خواهد کرد و بنابراین بازی قدم‌به‌قدم به نتیجه نهایی‌اش نزدیک می‌شود. شطرنج، هگز، نیم و … از این دسته‌اند. در حالت دوم که به آن بازی هم‌زمان[14] گفته می‌شود، نتیجه تصمیم بازیگران، حتی اگر بازیگران در زمان‌های متفاوت تصمیمشان را گرفته باشند، به‌صورت هم‌زمان بر روی یکدیگر تأثیر می‌گذارد.

یک مثال از بازی جمع-ناصفر

یک بازی جمع-ناصفر، با اطلاعات کامل و هم‌زمان، بازی مخمصه زندانی است. به این صورت که دو شریک جرم دستگیر و زندانی‌شده‌اند و هرکدام در فرایند اعتراف گیری قرار دارند. چون هرکدام از زندانی‌ها دو انتخاب دارند (سکوت یا اعتراف)، درمجموع چهار حالت ممکن وجود دارد. اگر هر دو اعتراف کنند به هشت سال زندان محکوم می‌شوند، اگر هر دو سکوت کنند به یک سال زندان محکوم می‌شوند و اگر فقط یکی از آن‌ها اعتراف کند، اعتراف کننده آزاد خواهد شد و آن‌که سکوت کرده به ده سال زندان محکوم خواهد شد. این اطلاعات در جدول 1 خلاصه‌شده است.

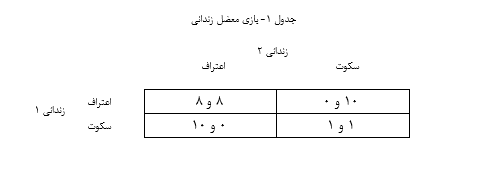
در جدول 1، نتیجه هر حالت در یک‌خانه از جدول به این صورت نشان داده‌شده است که عدد اول مقدار محکومیت زندانی اول و عدد دوم مقدار محکومیت زندانی دوم را تعیین می‌کند. قبل از آن‌که مشخص کنیم استراتژی هر بازیگر چه باید باشد، مشخص است که حتی اگر دو زندانی در دو زمان متفاوت تصمیم به عمل خود بگیرند، بازهم بازی بالا هم‌زمان است؛ زیرا هیچ‌کدام از زندانی‌ها از تصمیم دیگری آگاه نیست، مگر هنگامی‌که هردوی آن‌ها تصمیم خود را گرفته باشند.

برای آن‌که بفهمیم استراتژی بهینه برای یک زندانی چیست، ازاینجا شروع می‌کنیم که هر زندانی می‌خواهد تعداد سال محکومیتش را کم کند. زندانی اول کافی است دو حالت را در نظر بگیرد تا بداند در هر حالت چه کند: حالتی که زندانی دوم اعتراف می‌کند و حالتی که زندانی دوم سکوت می‌کند. در حالت اول اگر او هم اعتراف کند، به هشت سال زندان محکوم خواهد شد؛ اما اگر سکوت کند، محکومیت او ده سال خواهد بود. پس در این حالت به نفع اوست که اعتراف کند. در حالت دوم – زندانی دوم سکوت کند – اگر زندانی اول اعتراف کند، آزاد خواهد شد؛ اما اگر سکوت کند، به یک سال زندان محکوم خواهد شد؛ بنابراین در این حالت نیز به نفع اوست که اعتراف کند. ازآنجاکه در هر دو حالت اقدام او اعتراف خواهد بود، فارغ از این‌که زندانی دیگر چه می‌کند، اعتراف خواهد کرد. دقیقاً همین تصمیم را زندانی دوم نیز با تحلیل مشابه خواهد گرفت. نتیجه تحلیل‌های عاقلانه دو زندانی این خواهد بود که هر دو اعتراف کنند و به هشت سال زندان محکوم شوند. درحالی‌که اگر هر دو سکوت می‌کردند، نتیجه بهتری – یک سال زندان برای هرکدام – می‌گرفتند!

درس بزرگ این مثال این خواهد بود که تحلیل‌های عاقلانه همیشه به بهترین نتیجه ممکن برای همه افراد نمی‌انجامد، اما بااین‌حال بازهم انتخاب بازیگران عقلانی بوده است؛ اما در اینجا ممکن است این سؤال پیش بیاید که اساساً عقلانی بودن انتخاب کنشگران به چه معناست؟

نظریه بازی یک تعریف حداقلی از عقلانیتِ انتخاب را در نظر می‌گیرد؛ یک فرد رفتاری عاقلانه دارد اگر همیشه ترجیحات مشخصی داشته باشد و طبق این ترجیحات اقدامی را انتخاب کند؛ یعنی اگر x را به y ترجیح دهد، همیشه در رقابت بین این دو گزینه x را انتخاب کند. اگر چنین معنایی از عقلانیت در نظر گرفته شود، نظریه بازی به‌عنوان پیش‌فرض می‌پذیرد که کنشگران عاقل هستند. این برداشت از عقلانیت تا حدی با کاربرد معمول آن در زبان تفاوت دارد، اما مفروض گرفتن آن برای همه انسان‌ها امری دور از ذهن نیست.

آیا نتیجه غیرقابل‌باور مخمصه زندانی صرفاً پیامد عاقلانه بودن انتخاب کنشگران است؟ چرا بازی به این نتیجه رسیده است درحالی‌که هر دو کنشگر بر مبنای استراتژی بهینه رفتار کردند؟ آیا نباید انتظار داشت که استراتژی بهینه از سوی کنشگران به مطلوب‌ترین نتیجه در بازی – در این مثال، محکومیت یک سال زندان برای هر دو کنشگر – منتهی شود؟ برای پاسخ به این سؤالات باید به تمام پیش‌فرض‌هایی که در تحلیل بالا از این بازی موجود بود توجه کرد. برای مثال در این تحلیل فرض بر این بوده است که هر زندانی فقط و فقط به فکر کم کردن مجازات خویش است فارغ از این‌که بر سر زندانی دیگر چه خواهد آمد. همان‌طور که تاریخ نشان داده است، بسیاری از مجرمان چنان به ایدئولوژی و یا گروه خود معتقدند که حتی خود را فدای آن می‌کنند. برای چنین افرادی کاملاً محتمل است که به‌جای اعتراف سکوت کنند و بازی به نتیجه‌ای دیگر (سکوت از جانب هر دو زندانی) منتهی شود. درهرحال باید توجه داشت که این مفروضات نیز خود می‌توانند مدل شوند و با استفاده از نظریه بازی مورد تحلیل قرار گیرند. زیرا کماکان کنشگران عاقلانه رفتار می‌کنند؛ تفاوت در اینجاست که حفظ گروه برای آن‌ها اولویت بیشتری نسبت به حفظ خودشان دارد. پس هنوز هر بازیگر ترجیحاتی دارد و طبق ترجیحاتش عمل می‌کند. تنها تفاوت اینجاست که دیگر این ترجیحات مانند مثال قبل نیستند.

عقلانیت در نظریۀ بازی و کاربردهای مدل‌سازی نظریۀ بازی

نکته دیگری که از تعریف عقلانیت مشخص می‌شود آن است که منظور از عقلانیت این نیست که کنشگر لزوماً قبل از عمل خود تحلیل‌های ذهنی انجام دهد. گاهی اوقات چنین چیزی ممکن نیست؛ اما در این موارد نیز رفتاری عاقلانه از موجودات سر می‌زند. به این معنا که در بین گزینه‌های موجود برای عمل با فرض انتخاب دیگران، به‌طور بهینه انتخاب می‌کنند. این رفتار بهینه می‌تواند نتیجه تکامل باشد.

بنابراین پیداست که به‌سختی می‌توان به این پیش‌فرض نظریه بازی ایراد وارد کرد که انتخاب کنشگران عقلانی است. با این اوصاف این پیش‌فرض بی‌نقص نیست و طبق برخی دیدگاه‌ها می‌توان عیوب آن را آشکار کرد. به‌هرحال غالباً به‌طور حداقلی آن را می‌پذیرند؛ به‌عبارت‌دیگر دست‌کم در برخی حوزه‌ها – مثلاً بازار – رفتار کنشگران به این معنا عقلانی است، هرچند نمی‌توان با چنین فرضی همه واقعیات را توجیه کرد.

مدل‌سازی‌های نظریه بازی، فقط عقلانیت انتخاب کنشگران را پیش‌فرض نمی‌گیرد. هر مدل‌سازی بر مبنای پیش‌فرض‌هایی است که صدق آن‌ها – چه بر مبنای آزمایش‌های تجربی و چه بر مبنای افکار نیازموده – از پیش مسلم انگاشته می‌شود چراکه اساساً مدل‌سازی درصدد ساده کردن واقعیت‌های پیچیده است و برای توضیح یک پدیده، می‌خواهد عوامل نامربوط را تا حد ممکن حذف کند. درواقع کارایی یک مدل‌سازی خوب از یک پدیده، بسته به آن است که مهم‌ترین عوامل مربوط به آن پدیده و روابط آن‌ها با یکدیگر به‌درستی شناخته و تعریف شود تا مدل ساخته‌شده بتواند نمونه ساده‌شده‌ای از پدیده مورد نظر محسوب شود. به همین خاطر پژوهش‌های تأثیرگذار متعددی با استفاده از روش نظریه بازی وجود دارد که از ریاضیات بسیار ساده و قابل‌فهمی برای غیر ریاضی‌دانان استفاده کرده‌اند و علت اهمیت فوق‌العاده‌شان، در مدل‌سازی موفق آن‌ها بوده است. گاهی نیز این پیش‌فرض‌ها قابل‌بررسی دقیق‌ترند و حتی می‌توان آن‌ها را از پژوهش‌های تجربی نیز به دست آورد. برای مثال می‌توان با استفاده از آزمایش‌های اقتصاد رفتاری، تابع مطلوبیت کنشگران یک بازار را استخراج کرد و با واردکردن آن در یک مدل‌سازی ریاضیاتی، آن بازار را به‌عنوان یک بازی تحلیل کرد.

منابع برای مطالعه بیشتر

Morrow, J. D. (1994). Game theory for political scientists. Princeton University Press.

Osborne, M. J. (2004). An introduction to game theory (Vol. 3, No. 3). New York: Oxford university press.

McCarty, N., & Meirowitz, A. (2007). Political game theory: an introduction. Cambridge University Press.

Osborne, M. J., & Rubinstein, A. (1994). A course in game theory. MIT press.

Rogers, J. R. (2001). Information and judicial review: A signaling game of legislative-judicial interaction. American Journal of Political Science, 84-99.

Vanberg, G. (2001). Legislative-judicial relations: A game-theoretic approach to constitutional review. American journal of political science, 346-361.

Carrubba, C. J. (2009). A model of the endogenous development of judicial institutions in federal and international systems. The Journal of Politics, 71(1), 55-69.

Sanchez Urribarri, R. A., Schorpp, S., Randazzo, K. A., & Songer, D. R. (2011). Explaining changes to rights litigation: Testing a multivariate model in a comparative framework. The Journal of Politics, 73(2), 391-405.

[1] Theory of Games and Economic Behavior

[2] John Von neumann

[3] Oskar Morgenstern

[4] John Nash

[5] John Harsanyi

[6] Reinhard Selten

[7] Cooperative games

[8] Nash equilibrium

[9] Games of incomplete information

[10]Dynamic strategic interactions

[11]Zero-sum game

[12] Complete information

[13] Sequential game

[14] Simultaneous game